Python does not have a built-in double data type, but it does have a float type, which designates a floating-point number. You can consider these float values as doubles since they are typically represented in 64-bit ‘double-precision’ format, according to the IEEE 754 standard.

If you need more precision, numpy.float128 or numpy.longdouble can be used, depending on your system’s capabilities. However, it’s important to note that numpy.float128 may not always provide more precision than numpy.float64, especially on systems where the maximum floating-point precision is 64-bit. 

The maximum value of a floating-point number is approximately 1.7976931348623157e+308.

 Visual representation

Usage of double

data = 7.9

print(data)

print(type(data))

Output

7.9

<class 'float'>

The type() function confirms that the variable is of type float.

To use a decimal number (a floating-point number or equivalent to the double), you simply assign the decimal number to a variable:

number = 21.0

print(number)

Output

21.0

Using scientific notation

number = 21.1e2

print(number)

Output

2110.0

Using fractions module instead of floating-point numbers

from fractions import Fraction

print(Fraction(1, 3**54))

Output

1/58149737003040059690390169

Using decimal module

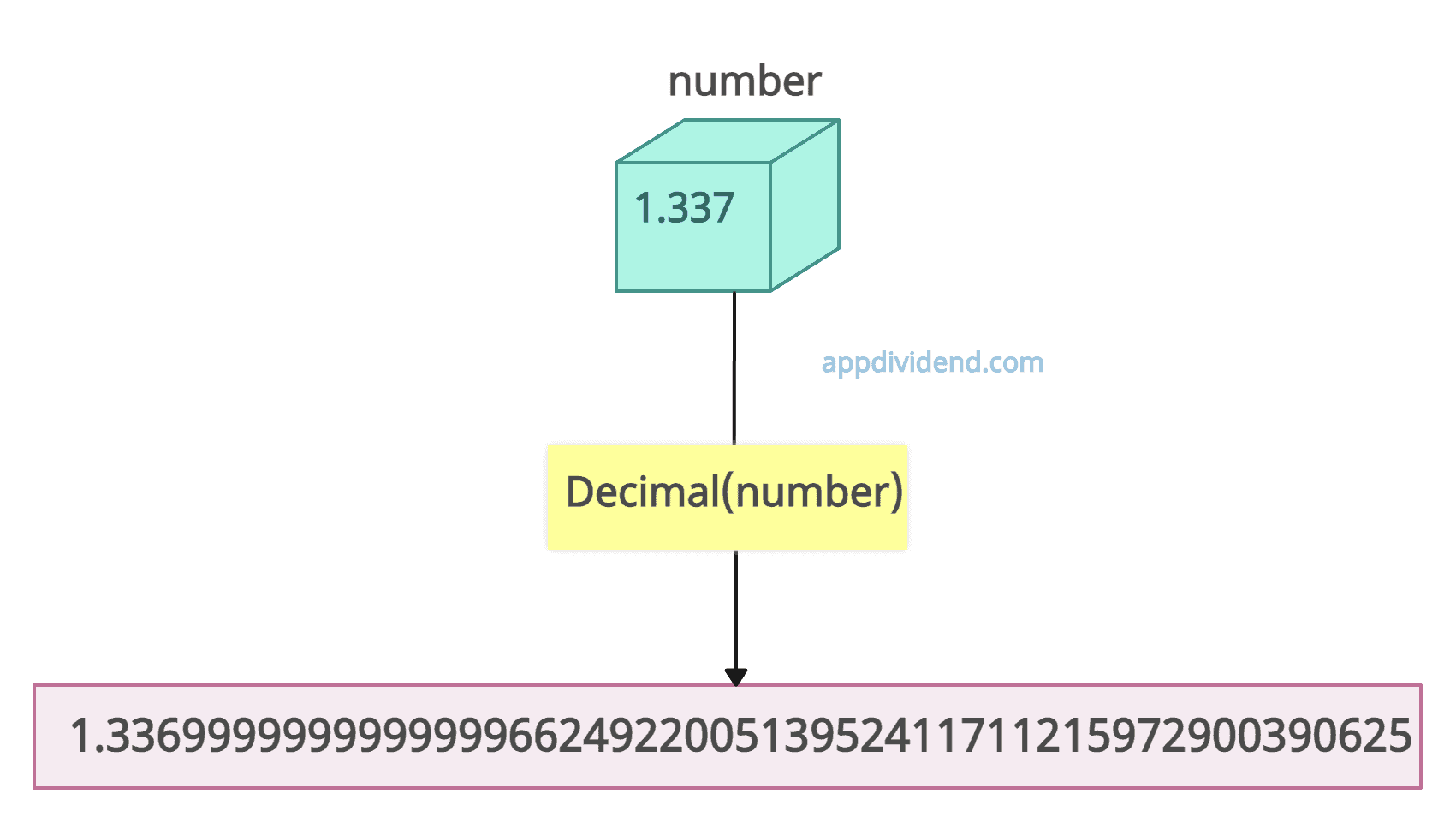
from decimal import Decimal 

print(Decimal(1.337))

Output

1.3369999999999999662492200513952411711215972900390625

To avoid this issue and use the precision benefits of the Decimal type, you should pass the number as a string.

from decimal import Decimal

print(Decimal('1.337'))

Output

1.337

That’s it.

Krunal Lathiya

With a career spanning over eight years in the field of Computer Science, Krunal’s expertise is rooted in a solid foundation of hands-on experience, complemented by a continuous pursuit of knowledge.