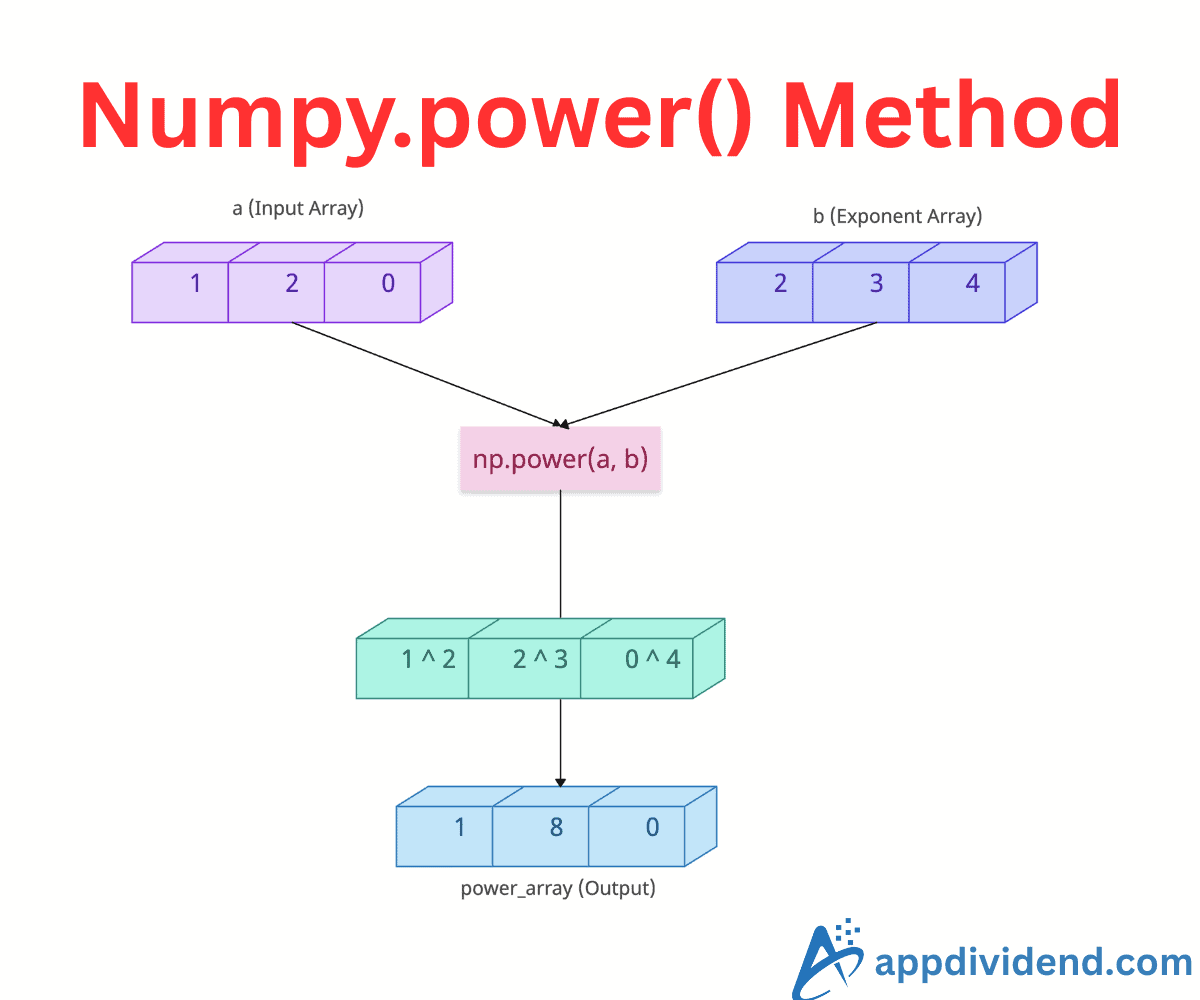
Numpy.power() method calculates the exponential value of each element in the first array raised to the power of the corresponding element in the second array. The second array can be an array or a scalar value.
import numpy as np x = np.array([2, 3, 4]) y = np.array([3, 2, 4]) power_array = np.power(x, y) print(power_array) # Output: [8 9 256]
In this code, np.power(x, y) performs element-wise exponentiation where each element in x is raised to the corresponding element in y. So, 2^3 (2*2*2) = 8, 3^2 (3*3) = 9, and 4^4 (4*4*4*4) = 256.
Syntax
numpy.power(x1,
x2,
out=None,
where=True,
casting='same_kind',
order='K',
dtype=None,
subok=True[, signature])
Parameters
| Argument | Description |
| x1 (required, array_like) | It represents a base array or scalar value. |
| x2 (required, array_like) | It represents an exponent that can be either an array or a scalar value. |
| out (ndarray, optional) | It is an output array to store the result. By default, its value is None. |
| where (optional) | It is a Boolean array condition that determines when operations are executed. |
| casting (optional) | It controls data casting (‘no’, ‘equiv’, ‘safe’, ‘same_kind’, ‘unsafe’).
By default, its value is “same_kind”. |
| order (optional) | It represents the memory layout of output (‘C’, ‘F’, ‘A’, ‘K’).
By default, it is ‘K’ (match input). |
| dtype (optional) | It overrides the data type of the result. |
| subok (optional) | If True, subclasses are passed through; otherwise, it forces the base-class array. |
Scalar component
Let’s take an input array and a scalar exponent and calculate the element-wise power.
import numpy as np arr = np.array([5, 10, 20]) power_array = np.power(arr, 2) print(power_array) # Output: [ 25 100 400]
In this code, we raised the first array to the power of 2. So, 5^2 = 25, 10^2=100, and 20^2=400. Hence, in the output, the array is [25, 100, 400].
Negative base with integer exponent
What if the base array contains negative values and the exponent is an integer? Let’s find out.
import numpy as np negative_array = np.array([-2, -3, -5]) exponent_array = np.array([2, 3, 3]) result = np.power(negative_array, exponent_array) print(result) # Output: [ 4 -27 -125]
If the exponent value is even, the corresponding output value will be positive even if the input value is negative because -2 x -2 = 4. But if the exponent is an odd value, the corresponding output value will be negative.
For example, -3x-3x-3 = -27, and last, -5x-5x-5 = -125.
Broadcasting
NumPy tries to align shapes from right to left in broadcasting.
Let’s say we have an input array of shape (3, 1) and exponent_array has a shape (3, ), the exponent_array will be broadcast to (1, 3), and then the power operation will occur, and the output shape will be (3, 3).
import numpy as np x1 = np.array([[1], [2], [3]]) # Shape (3, 1) x2 = np.array([1, 2, 3]) # Shape (3,) result = np.power(x1, x2) # Output shape (3, 3) print(result) # Output: # [[ 1 1 1] # [ 2 4 8] # [ 3 9 27]]
Here is the calculation:
Row 1 (x1=1):
[1**1, 1**2, 1**3] = [1, 1, 1]
Row 2 (x1=2):
[2**1, 2**2, 2**3] = [2, 4, 8]
Row 3 (x1=3):
[3**1, 3**2, 3**3] = [3, 9, 27]
Using out and where arguments
You can perform a masked operation using the “where” argument and save the output in a new array using the “out” argument.
import numpy as np a = np.array([1, 2, 3, 4]) b = np.array([3, 3, 3, 3]) out_arr = np.empty(4, dtype=int) np.power(a, b, where=(a % 2 == 0), out=out_arr) print(out_arr) # Output: [ 0 8 0 64]
In this code, we create a condition that raises the power of only the even values from the “a” array, not the odd values. So, in the output array, 2^3 = 8 and 4^3 = 64, and the rest of the values are 0.
That’s all!