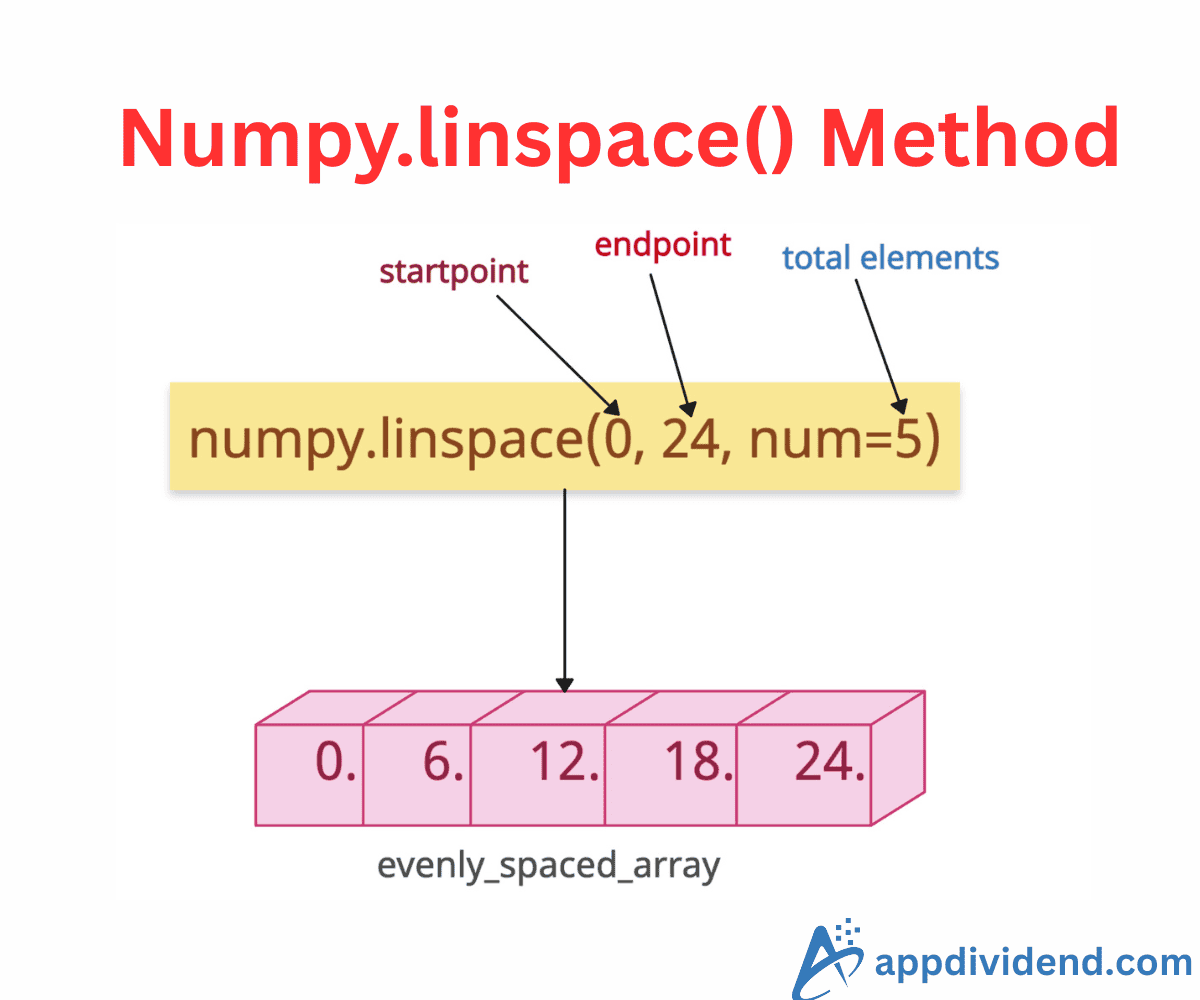
Numpy.linspace() method generates evenly spaced numbers over a specified interval. It returns an array of num equally spaced samples in the closed interval [start, stop] (by default) or the half-open interval [start, stop) If the endpoint is excluded.
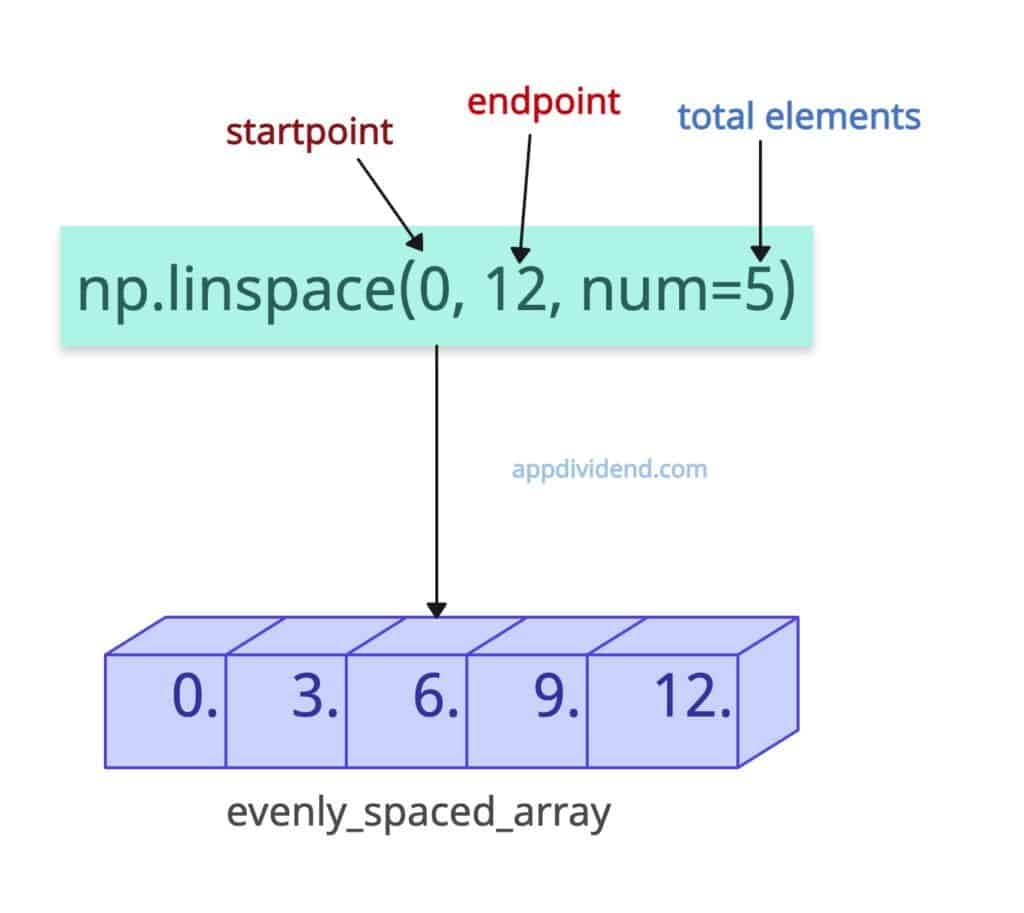
import numpy as np evenly_spaced_array = np.linspace(0, 12, num=5) print(evenly_spaced_array) # Output: [ 0. 3. 6. 9. 12.]
In this code, we created an array of five elements with even spacing between them from 0 to 12. Since we had already provided a number of samples to generate, step = 3 was automatically taken.
Here is the calculation for step size = (12 – 0) / (5 – 1) = 3.
The default dtype is float64 for NumPy arrays.
Syntax
numpy.linspace(start,
stop,
num=50,
endpoint=True,
retstep=False,
dtype=None,
axis=0)
Parameters
| Argument | Description |
| start (array_like or scalar, required) | It represents the starting value(s) of the sequence. |
| stop (array_like or scalar, required) | It represents the end value(s) of the sequence. |
| num (int, optional, default=50) | It is the number of samples to generate. |
| endpoint (bool, optional, default=True) | If endpoint = True, the stop is included in the sequence.
If endpoint = False, it generates num points up to but not including stop. |
| retstep (bool, optional, default=False) |
If True, it returns a tuple (samples, step), where step is the spacing between samples. |
| dtype (data-type, optional) | It defines the data type of the output array. |
| axis (int, optional, default=0) |
It is the axis along which to store the samples when start or stop are array-like. |
Default behaviour
If you only pass the starting and ending points to the np.linspace() method, it will create 50 samples, including both points. The reason is simple: by default, the number of elements is 50.
import numpy as np array = np.linspace(0, 5) print(array) # Output: # [0. 0.10204082 0.20408163 0.30612245 0.40816327 0.51020408 # 0.6122449 0.71428571 0.81632653 0.91836735 1.02040816 1.12244898 # 1.2244898 1.32653061 1.42857143 1.53061224 1.63265306 1.73469388 # 1.83673469 1.93877551 2.04081633 2.14285714 2.24489796 2.34693878 # 2.44897959 2.55102041 2.65306122 2.75510204 2.85714286 2.95918367 # 3.06122449 3.16326531 3.26530612 3.36734694 3.46938776 3.57142857 # 3.67346939 3.7755102 3.87755102 3.97959184 4.08163265 4.18367347 # 4.28571429 4.3877551 4.48979592 4.59183673 4.69387755 4.79591837 # 4.89795918 5. ]
As you can see from the output above, we have an array with 50 samples, including the first element 0, and the last element 5.
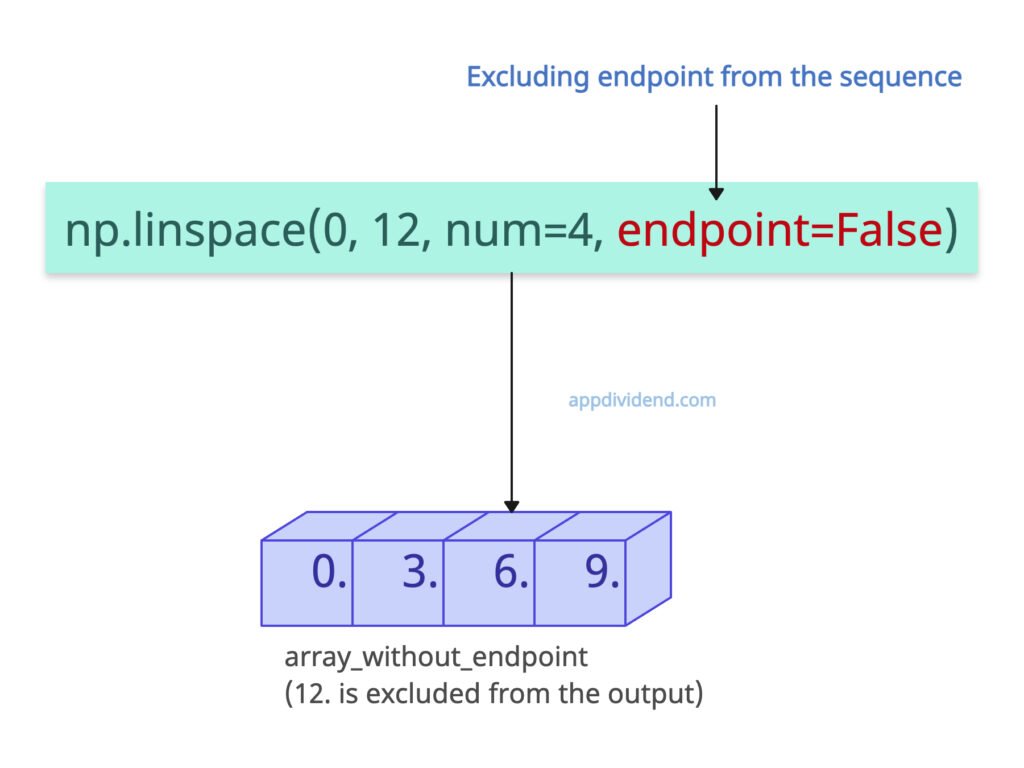
Excluding endpoint
Let’s exclude the endpoint from the generated array of sequence by passing endpoint=False argument.
import numpy as np array_without_endpoint = np.linspace(0, 12, num=4, endpoint=False) print(array_without_endpoint) # Output: [0. 3. 6. 9.]
In the above code, you can see that it did not include the endpoint value 12 in the output. It stopped at 9.
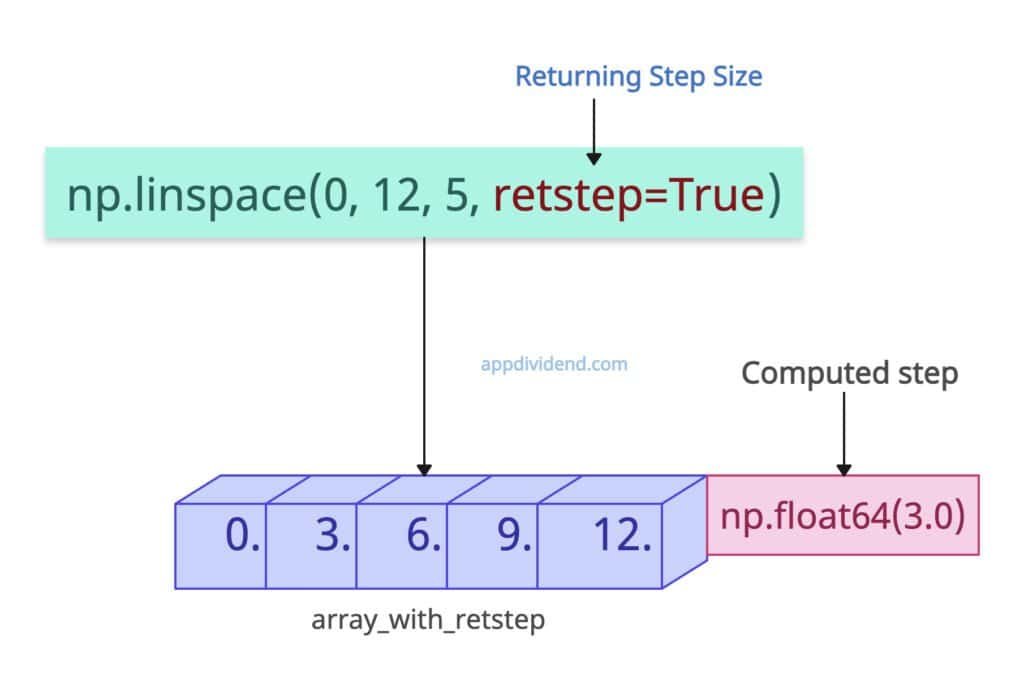
Returning Step Size
The “retstep” argument is helpful when you want an array with the computed step.
import numpy as np array_with_retstep = np.linspace(0, 12, 5, retstep=True) print(array_with_retstep) # Output: (array([ 0., 3., 6., 9., 12.]), np.float64(3.0))
In this code, you can see that the interval between the array values is 3.0. Therefore, the calculated step is np.float64(3.0), and hence we obtain this value in the output.
Specifying dtype (Integer)
Let’s pass the dtype=int argument to get the array of integers.
import numpy as np array_of_ints = np.linspace(0, 5, dtype=int, num=5) print(array_of_ints) # Output: [0 1 2 3 5]
The output array contains integers as expected instead of float64 values.
Multi-Dimensional with Axis=0
Let’s generate a 2D array with 3 evenly spaced samples between [0, 1] and [10, 20] along axis=0.
The axis=0 stacks values down rows (vertical growth).
import numpy as np array_axis_0 = np.linspace([0, 1], [10, 20], 3, axis=0) print(array_axis_0) # Output: # [[ 0. 1. ] # [ 5. 10.5] # [10. 20. ]]
In this code, np.linspace() calculates element-wise interpolation.
Passing axis=0 means stacking the generated samples along rows (downwards), which creates an array column-wise.
For the first column (0 to 10), it divides the interval [0, 10] into 3 evenly spaced values [0., 5., 10.].
For the second column (1 to 20), divide the interval [1, 20] into 3 evenly spaced values [1., 10.5, 20.].
Multi-Dimensional with Axis=1
Let’s generate a 2D array with 3 evenly spaced samples between [0, 1] and [10, 20] along axis=1.
The axis=1 stacks values across columns (horizontal growth).
import numpy as np array_axis_1 = np.linspace([0, 1], [10, 20], 3, axis=1) print(array_axis_1) # Output: # [[ 0. 5. 10. ] # [ 1. 10.5 20. ]]
Passing axis=1 means NumPy stacks the samples horizontally (across columns). Each input element ([0, 1] and [10, 20]) expands across its row.
For the first row (0 to 10), it divided the interval [0, 10] into 3 evenly spaced values [0., 5., 10.].
For the second row (1 to 20), it divided the interval [1, 20] into 3 evenly spaced values [1., 10.5, 20.].
np.linspace() vs np.arange()
The main difference between np.linspace() and np.arange() is that the arange() method stops before exceeding stop, while linspace() guarantees an exact number of evenly spaced points.
import numpy as np
array_arange = np.arange(0, 1, 0.2)
array_linspace = np.linspace(0, 1, 6)
print("arange:", array_arange)
# Output: [0. 0.2 0.4 0.6 0.8]
print("linspace:", array_linspace)
# Output: [0. 0.2 0.4 0.6 0.8 1. ]
You can see from the above code that np.linspace() contains 1.0, while np.arange() does not because in linspace() the last argument 6 is the total number of elements in the output, whereas in the case of arange(), the last argument 0.2 is the step, or you can say an interval.
That’s all!