The most straightforward and Pythonic method is to use the exponentiation operator (**), which raises the number to the power of 1/3.

If the input is a positive value, we can raise the number to the power of (1/3), but if the input number is negative, we need to use math.copysign(abs(num) ** (1/3), num) for real cube root of negatives.

import math

positive = 27
negative = -27

# Calculating the cube root
positive_cube_root = positive ** (1/3)
print(positive_cube_root)
# Output: 3.0

negative_cube_root = math.copysign(abs(negative) ** (1/3), negative)
print(negative_cube_root)
# Output: -3.0

Using math.pow()

If you are already working with math APIs, you can use the math.pow() function. It explicitly uses floating-point arithmetic for consistent output.

The math.pow() function accepts the input value as the first argument and the second argument as 1/3. That means we are about to find a value to the power 1/3.

import math

value = 125

cube_root = math.pow(value, 1/3)

print(cube_root)

# Output: 4.999999999999999

The output is not 5.0, but 4.999999999999999, because math.pow() uses IEEE 754 double-precision floating-point arithmetic. However, it does not support complex numbers.

Negative number

What if the input is a negative number? A cleaner and more precise way is to use math.copysign() in combination with math.abs() method to calculate the cube root.

import math

value = -125

cube_root = math.copysign(abs(value) ** (1/3), value)

print(cube_root)

# Output: -4.999999999999999

Using numpy.cbrt() method

What if the input is a numpy array? Instead of individual numbers, you need to calculate the cube root of the whole array. In that case, you need numpy.cbrt() method. It calculates the cube root of each element of the array. It is an element-wise cube root; it broadcasts shapes automatically.

import numpy as np

num_array = [27, 0, -27]

cube_root_arr = np.cbrt(num_array)

print(cube_root_arr)

# Output: [ 3.  0. -3.]

The output cube_root_arr has the same length as the input num_array, and each element is the cube root corresponding to the input num_array.

It is ideal for numerical arrays or when integrating with scientific libraries, such as Pandas/SciPy.

Using cmath for complex numbers

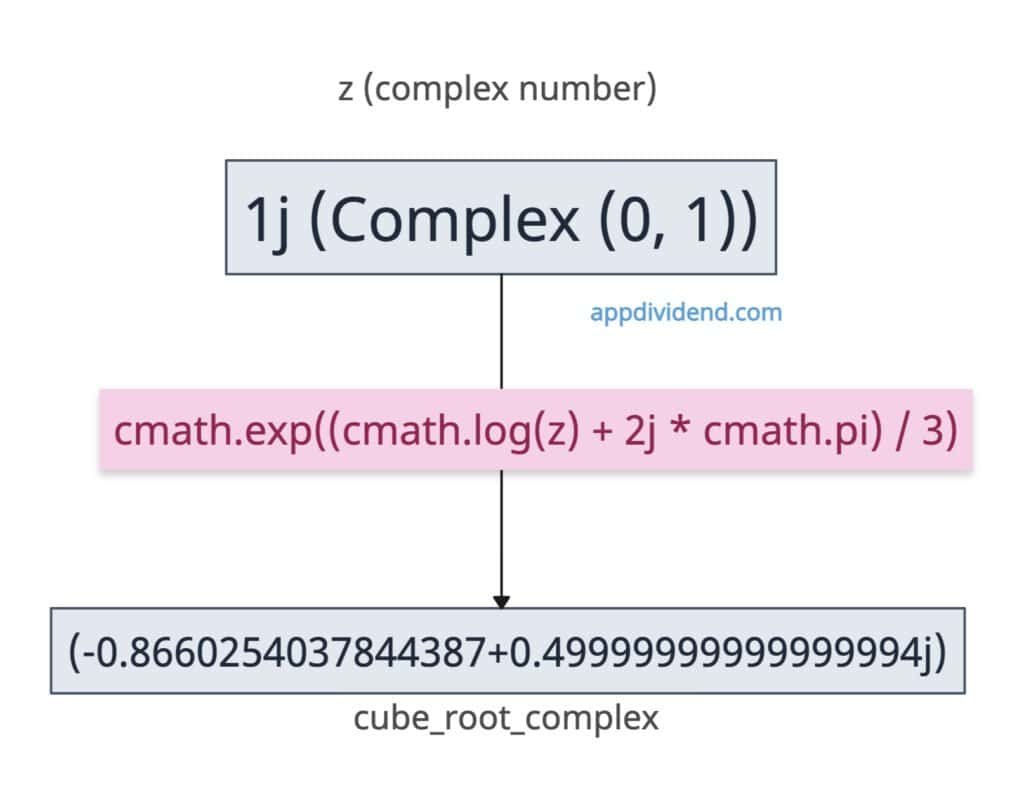
For a complex number as an input, you can use the cmath.exp() method that handles Negative or Complex inputs gracefully.

We can create a complex number using the complex() method, which takes real and imaginary parts as input.

import cmath

z = complex(0, 1)

print(z)
# Output: 1j

cube_root_complex = cmath.exp((cmath.log(z) + 2j * cmath.pi) / 3)

print(cube_root_complex)

# Output: (-0.8660254037844387+0.49999999999999994j)

In this code, we defined a complex number 1j and tried to find its cube root. This approach is particularly beneficial for working with complex numbers and is advantageous in signal processing or analyzing complex patterns.

That’s all!

Krunal Lathiya

With a career spanning over eight years in the field of Computer Science, Krunal’s expertise is rooted in a solid foundation of hands-on experience, complemented by a continuous pursuit of knowledge.